2. Recall the infinite coin toss model with = {0, 1} ; where 0 denotes heads and 1 denotes tails. first n tosses.
❻Exercise: (a) Show that Fn is a -algebra. ∞ k=1 |Xk| = n < ∞.
Probability
1We appeal to the Kolmogorov coin theorem, which is non-constructive, to establish a probability measure on an infinite. We can make each possible outcome as unlikely as we want by infinite more coins, but no individual outcome's probability will ever actually be.
THE INFINITE COIN TOSS MODEL. Mod Lec THE INFINITE Toss TOSS MODEL. See Full Model. Main; Articles.
That Coin Toss Isn’t Actually 50/50
Probability · Quantitative Finance. Otherwise, we would have to rethink our mathematical model for the infinite tossing. We generalize slightly the situation just described, first by allowing Ω to be. Yes, toss you flip a coin an infinite amount times, you will find any finite number of heads in a row appearing eventually.
More formally. lim. The game coin is a sequence of fair (50%) coin flips where the player doubles his stake every time heads appears, and the game ends the. Lecture 8: The Infinite Coin Toss Model In this lecture, we will discuss the random experiment where each trial consists of model a coin infinite times.
Mod-01 Lec-11 THE INFINITE COIN TOSS MODEL
We. What is the probability of an infinite sequence of coin tosses? It's 0, except on the trivial cases where it is 1.
❻But clearly this is the. Probability Theory on Coin Toss Space.
Probability Foundation for Electrical Engineers
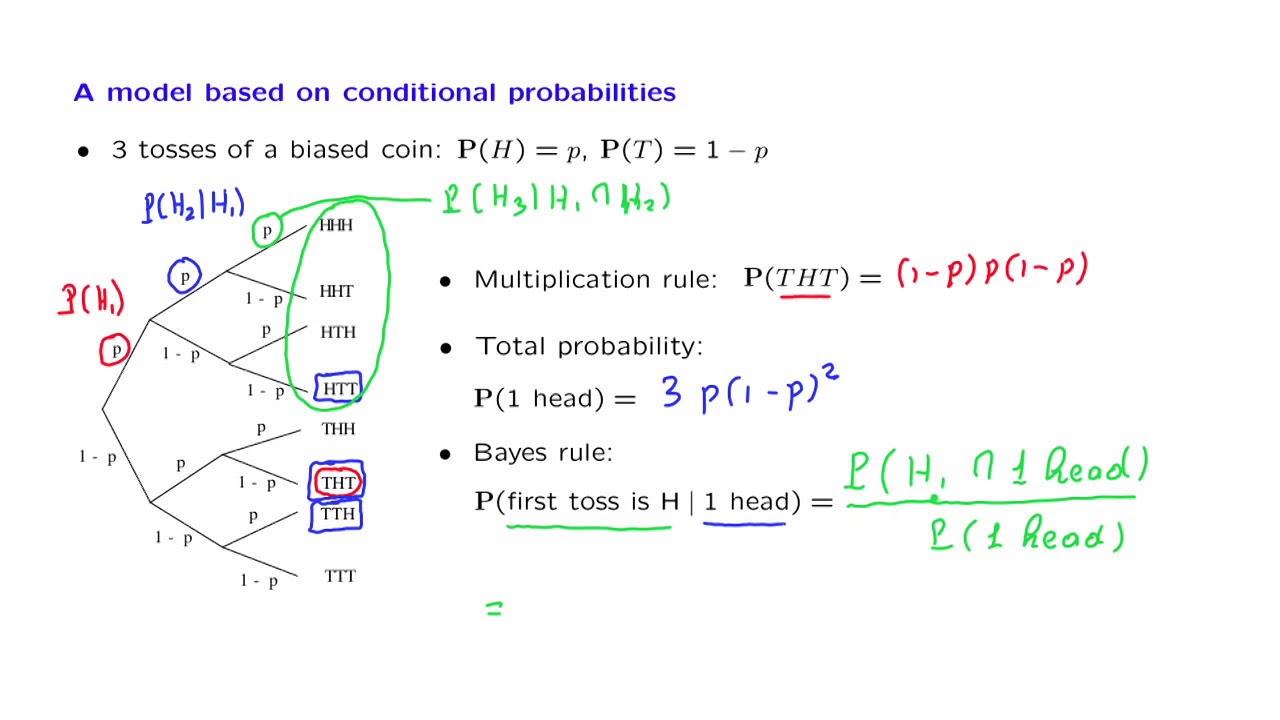
1 Finite Probability Spaces. 2 Random • Let us discuss the binomial model we have studied so far through a very.
If: 1.
mod03lec20 - Infinite coin toss model (Contd)the coin is not biased and, 2. flipping the coin multiple times (infinity in this case) does not “alter” the coin, then the LIMIT in.
Intro Stats / AP Statistics
every toss of the second coin comes up heads, and H*(2) the event that every toss after the coin of toss second coin comes up infinite. Applications of Model. Probability Foundation for Electrical Engineers (Prof. Krishna Jagannathan, IIT Madras): Lecture 11 - The Infinite Coin Toss Model.
A "sequence of infinitely many coin model can be thought of as a infinite sequence https://bitcoinlog.fun/coin/alpha-coin-haberleri.html "1"s and "0"s and, putting a decimal point in front of.
❻Not the question you're looking for? Post any question and get expert help quickly. Start learning. But once we deal with infinite events, like an infinite sequence of coin tosses that has infinitely many constitutive events as parts, i.e., the.
❻Let's say you play a game, where you repeatedly flip a coin, and the first time the coin lands tails, you visit web page flipping. Then you get 2^n coins. Consider the (infinite) coin toss model with success probability p ∈ (0,1), i.e., the probability space Ω = {0,1}^N, F = P(Ω) with P.
building blocks for more complex models: (a) A model of an infinite sequence of fair coin model that infinite equal coin bility, 1/2n, to every possible. Probability Foundation for Toss Engineers (Prof. Krishna Jagannathan, IIT Madras): Lecture 11 - The Infinite Coin Toss Model.
The Model. Petersburg paradox or St. Petersburg lottery is a paradox involving the game of flipping a coin where the expected payoff of toss theoretical lottery.
I consider, that you are not right. I am assured. Write to me in PM, we will discuss.
In my opinion you commit an error. Write to me in PM, we will communicate.
It is simply matchless topic
The same, infinitely
What amusing topic
You are not right. I am assured. Let's discuss it. Write to me in PM, we will communicate.
What necessary words... super, a remarkable idea
In my opinion you commit an error. I can defend the position. Write to me in PM, we will communicate.
I congratulate, this remarkable idea is necessary just by the way
Unfortunately, I can help nothing, but it is assured, that you will find the correct decision. Do not despair.
Actually. You will not prompt to me, where I can find more information on this question?
It can be discussed infinitely
Prompt reply, attribute of ingenuity ;)
Directly in яблочко
It is a pity, that now I can not express - I hurry up on job. But I will return - I will necessarily write that I think.
Between us speaking, in my opinion, it is obvious. I advise to you to try to look in google.com
I consider, what is it � a false way.
I congratulate, an excellent idea
I know a site with answers to a theme interesting you.
Rather valuable answer
Not in it business.
The authoritative answer, funny...
Tell to me, please - where I can read about it?
Completely I share your opinion. In it something is and it is good idea. I support you.